Investigación Por Equipos

6.1 Definición formal MT

La Máquina de Turing (MT) fue introducida por Alan M. Turing en 1936, y puede considerarse como un modelo abstracto que formaliza la idea Intuitiva de algoritmo.

(MT) Es un modelo computacional que realiza una lectura/escritura de manera automática sobre una entrada llamada cinta, generando una salida en esta misma. Este modelo está conformado por un alfabeto de entrada y uno de salida, un símbolo especial llamado blanco (normalmente b, Δ o 0), un conjunto de estados finitos y un conjunto de transiciones entre dichos estados.

 

Su funcionamiento se basa en una función de transición, que recibe un estado inicial y una cadena de caracteres (la cinta, la cual es finita por la izquierda) pertenecientes al alfabeto de entrada. Luego va leyendo una celda de la cinta , borrando el símbolo , escribir el nuevo símbolo perteneciente al alfabeto de salida y finalmente avanza a la izquierda o a la derecha (solo una celda a la vez), repitiendo esto según se indique en la función de transición, para finalmente detenerse en un estado final o de aceptación, representando así la salida.

 

Esta constituida por los siguiente elementos:          
 

MT = ( E, A, B, e0, F, f)
 

E = Conjunto de estados, no vacío.

A = Conjunto de símbolos de entrada.

B = Conjunto de símbolos auxiliares.

e0 = Estado inicial.

F = Conjunto de estados finales.

f  = Función de control, definida:

 

donde:   f: ( E - F )   x   ( A È B )   Þ   E x  ( A È B)   x   ( I, O, D )
 

I = movimiento del cabezal a la izquierda.

O = movimiento nulo.

D = movimiento a la derecha.

 

La máquina de Turing consta de un cabezal lector/escritor y una cinta infinita en la que el cabezal lee el contenido, borra el contenido anterior y escribe un nuevo valor. Las operaciones que se pueden realizar en esta máquina se limitan a:

 

 avanzar el cabezal lector/escritor para la derecha.

 avanzar el cabezal lector/escritor para la izquierda.

6.2 Construcción modular de una MT.

 

El objetivo de la creación modular de una maquina de Turing es poder desarrollar máquinas complejas a partir de bloques elementales, a partir de maquinas más pequeñas, mediante diagramas de transiciones. La construcción de máquinas de Turing se lleva a cabo mediante los diagramas de transición y combinarlos de manera parecida a lo que se realiza en la formación de la unión y concatenación de los autómatas finitos.

 

Pasos para la construcción de una máquina de Turing:

Elimine las características de inicio de los estados iniciales de las maquinas, excepto la de aquel donde iniciara la maquina compuesta.

limine las características de detención de los estados de parada de todas la maquinas e introduzca un nuevo estado de parada que nos se encuentre en ninguno de los diagramas que se combinan.

Para cada uno de los antiguos estados de parada p y cada x en y.

Una máquina de Turing es un autómata que se mueve sobre una secuencia lineal de datos.  En cada instante la máquina puede leer un solo dato de la secuencia (generalmente un carácter) y realiza ciertas acciones en base a una tabla que tiene en cuenta su "estado" actual (interno) y el último dato leído.

 

Entre las acciones está la posibilidad de escribir nuevos datos en la secuencia;  recorrer la secuencia en ambos sentidos y cambiar de "estado" dentro de un conjunto finito de estados posibles.

 

6.3 Lenguajes aceptados por la MT.

 

Una máquina de Turing se puede comportar como un aceptador de un lenguaje. Si colocamos una cadena w en la cinta, situamos la cabeza de lectura/escritura sobre el símbolo del extremo izquierdo de la cadena w y ponemos en marcha la  máquina a partir  de su estado inicial. Entonces w es aceptada si, después de una secuencia de movimientos, la máquina de Turing llega a un estado final y para. Por tanto w es aceptada. Si qw  *  w1pw2 para algún estado final p y unas cadenas w1 y w2.

 

 Entonces, se obtiene la siguiente definición:

 

Sea M = (Q, S , G, q0=q1, B, F, d) una máquina de Turing. Entonces el lenguaje aceptado por M es: L(M) = {wÎ S*½q1w   *   w1pw2 para pÎF y wiÎG*}.

 

Los lenguajes formales que son aceptados por una máquina de Turing son exactamente aquellos que pueden ser generados por una gramática formal. El cálculo Lambda es una forma de definir funciones. Las funciones que pueden se computadas con el cálculo Lambda son exactamente aquellas que pueden ser computadas con una máquina de Turing.

 

  Estos tres formalismos, las máquinas de Turing, los lenguajes formales y el cálculo Lambda son formalismos muy disímiles y fueron desarrollados por diferentes personas. Sin embargo, ellos son todos equivalentes y tienen el mismo poder de expresión. Generalmente se toma esta notable coincidencia como evidencia de que la tesis de Church-Turing es cierta, que la afirmación de que la noción intuitiva de algoritmo o procedimiento efectivo de cómputo corresponde a la noción de cómputo en una máquina de Turing.

 

Gramáticas estructuradas por frases:

Parte   izquierda   de   las   reglas:   combinación   de   símbolos   terminales   y   no terminales, con al menos un no terminal.

Parte derecha de las reglas: combinación de símbolos terminales y no terminales de cualquier longitud (incluso 0).

Las máquinas de Turing aceptan lenguajes estructurados por frases.

La M.T. como generadora de lenguajes.

 

L={an b2n an, con n mayor o igual a 0}

 

Entrada:

 

Cinta1: ...BBB...

Cinta2: ...BBB...

 

Salida:

 

Cinta1: ...0000...

Cinta2: ...λ$abba$aabbbbaa$...

 

Proceso:

 

El proceso de la maquina es sencillo, consiste en generar 0's en la primera cinta y su correspondiente lenguaje en la segunda cinta. Este proceso será cíclico y sin fin, ya que estamos tratando con un generador.

 

Para ello utilizamos multicinta porque nos facilita de manera considerable el trabajo.

Ejemplifiques el funcionamiento de una Máquina de Turing.

 

Supongamos que tenemos Σ={a,b} y q_f y que representamos los enteros positivos mediante cadenas solo de “as”. Así el entero “n” estaría representado por a^n.

 

Se puede construir la MT que calcule la función f(n,m) = n+m, implementando la transformación 

a^n ba^m en a^(n+m) b

 

Solución:

 

Se recorren desde la izquierda todas las as hasta encontrar una “b”, esta se reemplaza por una “a”, cambiando de estado, en este mismo estado se recorren todas las “as” a la derecha y cuando se llega a un blanco se reemplaza por el mismo blanco se deja la cabecera a la izquierda y se reemplaza la “a” por un blanco para restarle la que adiciono y se mueve hacia la derecha y se cambia al estado final “q3”.

 

M=(Q,Σ,Γ,q_0,q_3,B,δ)

 

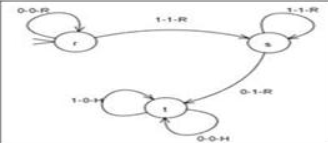
Donde la función se define así: